如果以黑洞的体积来计算其密度，体积越大其密度将越小

2019-04-01 09:09:08来源：科普大世界

黑洞的密度有多大?如果把我们的地球压缩成一个黑洞，那么它的体积将只有直径1.8厘米，相当于一个小玻璃球那么大，这样的密度是不是让人叹为观止?

如果将我们的地球压缩成中子星，那么它的直径将在22米左右，如果压缩成白矮星，其直径大概在二三十公里左右，很显然，同样的质量之下，黑洞的密度最大。

然而这样的说法却又是不严谨的，因为小质量的黑洞和大质量黑洞的密度完全不同，也就是说黑洞的密度并不是一个固定值，而是变化极大，体现为质量越大的黑洞的密度越小，很是有点匪夷所思。

计算黑洞体积的大小，有一个史瓦西半径公式，是从物体逃逸速度的公式衍生而来，通常物体的速度若小于一个天体的逃逸速度，就不能摆脱其引力束缚，会被该天体吸引，无法脱离轨道而逃逸到星际空间。所以当特定质量的物质被压缩到黑洞的该半径值之内，将没有任何已知类型的力可以阻止该物质在自身引力的条件下将自己压缩成一个黑洞。

黑洞的史瓦西半径公式为：Rs = 2GM/c^2 ; 其中Rs为史瓦西半径，G为引力常数，M为星体质量，c为光速。

如果仅从史瓦西半径看，所有半径尺度和质量大小的黑洞的都是可能存在的，而且黑洞的半径与质量成正比，又因为球体体积与半径的立方成正比，那么当黑洞质量增加时，体积的增加程度将大于质量，这样黑洞的密度就会变小，因此当黑洞的质量达到一定程度时，密度就会很小。

比如如果将太阳你要说成一个黑洞，那么史瓦西半径计算其半径将为3000米左右，也就是说太阳会成为一个直径6公里左右的黑洞，但是我们知道地球的质量相当于太阳的33万分之一，体积是地球130万倍，同比例的话，太阳变成黑洞的体积应该也是地球的33万倍，然而很显然，一个直径6公里左右的大球中，能放下的直径1.8厘米的玻璃球的数量远不止33万个，也不是130万个，就是33亿个也不止，数量可达百万亿。

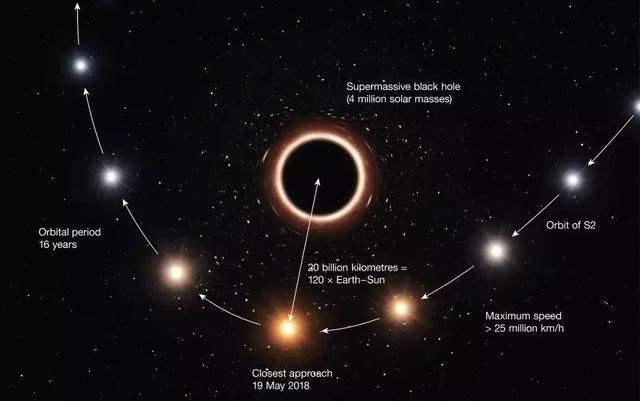
再如银河系中心黑洞的直径约为4500万公里，其质量约为太阳的431万倍，那么计算一下就会发现，银河系中心黑洞的体积也远超过431万个太阳变成黑洞的直径6公里的体积。

还有人计算发现，如果把我们银河系的质量看着一个黑洞的话，那么它的密度比空气还稀薄，而如果把我们的宇宙的质量看作一个黑洞，那么它的密度也大概就是每立方厘米中有5个原子，比我们所谓的真空还有空虚得多，不过它将和我们宇宙的密度几乎一样，这也就是说如果我们的宇宙是个黑洞的话，那么这个黑洞的体积几乎和我们的宇宙一样大。

所以，如果以黑洞的体积来计算其密度，那么黑洞的质量越大，或者说体积越大其密度将越小。

不过我们必须要明白的是，我们所说的黑洞的体积都是一个虚拟体积，因为这种定义和计算方法都是以黑洞的史瓦西半径来说的，史瓦西半径的最外端就是黑洞的视界边缘，然而它并非黑洞的实体界面，这只是一种虚拟体积概念，实际上一般认为黑洞的物质集中地是其内部的奇点，但是我们对黑洞中的世界还一无所知，只是推断认为黑洞中的奇点是密度无限大体积无限小的点，它的密度肯定是要高过中子星的，和黑洞的视界体积密度也完全不同。

标签：黑洞的体积黑洞的密度

如果以黑洞的体积来计算其密度，体积越大其密度将越小

相关阅读

精彩推荐

阅读排行

相关词

推荐阅读